Особенности использования индукционного нагрева цилиндрических деталей, сопряженных с осью

УДК 621.03.023: 621.77.014

Особенности использования индукционного нагрева
цилиндрических деталей, сопряженных с осью

В.И.Дудин, С.А.Лелехов, А.Н.Фещуков

Общество с ограниченной ответственностью
«Научно-производственная компания «ТомИндуктор»,
Москва, Томск, Российская Федерация

АННОТАЦИЯ

Введение. Представлены результаты расчетно-теоретического и экспериментального исследования вопроса о разъединении цилиндрической детали от оси при индукционном нагреве. Предметом изучения была температура разъединения цилиндрической детали от оси и ее зависимость от величины натяга и мощности индукционного нагрева.

Материалы и методы. Предметом изучения была температура внешней поверхности цилиндрической детали, при которой натяг равняется нулю и деталь снимается без усилия. С этой целью численно решали уравнения теплопроводности и деформации и определяли температуру разъединения. Одновременно рассчитывали температурный профиль по сечению цилиндрической детали.

Результаты. Зависимость температуры разъединения от мощности имеет две области: для относительно малых значений мощности температура разъединения практически постоянна, а для более высоких значений температура разъединения пропорциональна мощности. Полученные зависимости связаны с зависимостью коэффициента температуропроводности от температуры. С зависимостью коэффициента температуропроводности от температуры также связаны особенности посадки цилиндрических деталей на оси и валы. В значительной степени экспериментальный опыт авторов связан с внедрением высокочастотных индукционных нагревателей в железнодорожной отрасли: депо на всех железных дорогах системы ОАО «РЖД», на железнодорожных ремонтных заводах системы АО «Желдорреммаш».

Обсуждение и заключение. Полученные результаты позволяют рекомендовать в конструкции индукционных нагревателей иметь возможность контролировать мощность индукционного нагрева и время нагрева. Это позволит на техническом уровне запретить выполнение операций с выходом параметров за пределы регламента, что позволит увеличить надежность выполнения операций. Закономерности посадки цилиндрических деталей на оси и валы имеют важное технологическое значение, но требуется дополнительное теоретическое и экспериментальное исследование.

Ключевые слова: съем и посадка цилиндрических деталей, натяг, мощность индукционного нагрева, температура разъединения, температурный профиль, температуропроводность.

Введение. В нашей работе [1] были представлены результаты расчетно-теоретического исследования вопроса о нагреве и деформации цилиндрической детали, связанной натягом с осью, при индукционном нагреве. Расчеты проводили численными методами на основе простой модели: цилиндр, сопряженный натягом величиной d с осью. Внешний радиус цилиндра R₀, внутренний r₀, высота h. Электромагнитное поле частоты ω создает однослойный индуктор, витки которого расположены вдоль высоты. Расчетная схема представлена на рис. 1.

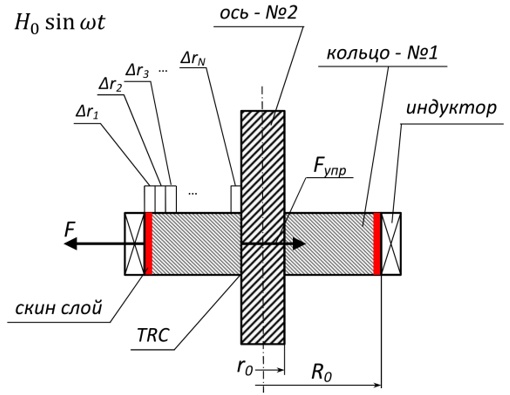
Рис. 1. Расчетная схема

Совместно решали уравнения теплопроводности и смещений [2,3]

dT(r,t)/dt=(λ/c·γ)·(d²T(r,t)/dr²) + 1/r(dT(r,t)/dr) + Q(r,t)           (1),

d²u(r,t)/dr² + 1/r(d(u(r,t)/dr) -u/r=(μ+1)∙α∙dT(r,t)/dr)               (2),

где: T(r,t) – профиль температуры по сечению кольца, а u(r,t) – соответствующее распределение смещений, λ- теплопроводность, Вт/м·K, с-теплоемкость, Дж/кг·K, γ-плотность материала кольца, кг/м³, Q(r,t) –  внутренний источник тепловыделений, связанный с индукционными токами, μ – коэффициент Пуассона. При численном решении уравнения ф.(1,2) использовали приближения:

1. Теплоизлучением в окружающую среду пренебрегали. Перенос тепла вдоль оси считали не существенным для результатов. В этих приближениях можно было использовать одномерную геометрию, т.е. температура и смещения зависели от одной компоненты, от радиуса r.

2. Все указанные характеристики материала при расчетах зависели от температуры, равно как и магнитная проницаемость еще зависела от индукции магнитного поля. Справочные данные вносились в приложения программы. Данные о значениях констант и их температурной и зависимости от индукции магнитного поля брали из общедоступных источников [4,5].

3. Использовали приближение Штейнметца [6], которое заключается в том, что тепловыделения вследствие протекания индукционных токов равны тем, которые вызывались бы постоянным током с амплитудой I₀=j₀sh, текущим в скин – слое. Здесь j₀ ̶ плотность индукционного тока при r=R₀, s – величина скин-слоя, h – высота кольца (цилиндра). Это дает возможность определить источник тепловыделений Q(r,t), что упрощает процедуру численного интегрирования уравнений теплопроводности и смещений. Кроме того, этот подход определяет структуру разбиений сечения на N отрезков для численного решения, причем (R₀-r₀)/N больше величины скин — слоя. Величина скин — слоя рассмотренных сталей в диапазоне 3-10кГц изменяется в диапазоне 0,36 — 0,66 мм. Так для кольца толщиной 14мм при разбиении получали 10 слоев. Начальное условие для всех слоев T_i=T₀=20⁰C(293К).

4. В приграничном слое, там где соприкасаются кольцо и ось учитывали тепловое сопротивление контакта (коэффициент TRC), связанное с натягом.

Определяли температуру внешней поверхности кольца, при которой натяг равнялся нулю. Эту температуру назвали температурой разъединения T_р. Помимо теоретического интереса следует отметить, что практически эту температуру просто измерять в эксперименте.  Проверка модели расчета [1] показала, что она дает адекватные ответы на вопросы: как время съема (здесь и далее – это время от начала нагрева до момента разъединения кольца и оси) зависит от мощности P индукционного нагрева, как указанное время съема зависит от тока индуктора, а значит от мощности индукционного нагрева, как изменяются во время нагрева контактное давление между цилиндром и осью, как изменяется температура внутренней поверхности цилиндра и т.д. Следует отметить, что в работе представлены в основном результаты расчетно-теоретического исследования. Это связано с двумя обстоятельствами. Первое, в настоящее время не выпускаются индукционные нагреватели с возможностью регистрации мощности. Поэтому, для такой регистрации необходимо дополнительное оборудование. Второе, мы использовали общедоступные данные по значениям материальных показателей [4,5].

Следует отметить, что использование индукционного нагрева имеет широкое распространение. Но публикаций на эту тему довольно мало. В этой связи следует отметить работу [7], где исследуется вопрос о нагреве индукционными методами стрелочных переводов в зимний период. Работа стрелок непосредственно связана с безопасностью движения транспортных средств на железных дорогах. Не менее важным является состояние внутренних колец подшипников ступиц колесных пар и опорных узлов локомотивов и вагонов, которые для обследования снимаются для контроля их состояния. Съем и последующую посадку внутренних колец подшипников в железнодорожной отрасли России, проводят индукционными нагревателями. Представленные материалы напрямую связаны с этими операциями.

Предмет исследования. Предметом наших расчетов было исследование зависимости температуры разъединения кольца и оси от мощности индукционного нагрева T_р(P). Эта зависимость определяется распределением температуры по сечению кольца, т. е. определяется физическими процессами, происходящими в кольце. Мощность тепловыделений в кольце также зависит от частоты ω переменного тока индуктора, т. е. температура разъединения может зависеть от частоты. Изменять мощность индукционного нагрева можно с помощью изменения тока индуктора, однако, в настоящее время не существует сильноточных индукционных нагревателей, в которых можно произвольно менять частоту переменного тока индуктора.

Также значительный практический интерес имеется к определению зависимости мощности индукционного нагрева, при которой кольцо снимается без натяга (d=0), от величины натяга.

Следует отметить следующее обстоятельство. Работа A, совершаемая против упругой силы F_упр при снятии натяга величиной d определяется из уравнения

 A=Pt=const                         (3),   

t– время нагрева, для данной величины натяга. Понятно, что время нагрева для данного натяга обратно пропорционально мощности [1].

Ясно, что формальный параметр T_р(r) – температура внешней поверхности кольца, при которой натяг d=0 и зависимость мощности индукционного нагрева P(d) от натяга определяются физическими процессами, происходящими в кольце при нагреве. Поэтому мы рассчитывали зависимость температуры в сечении кольца от радиуса, т. е. температурный профиль в момент достижения состояния с d=0.

Результаты. На рис. 2 представлены графики зависимости температуры T_р кольца № 42726 (подшипник ступицы электропоезда с диаметром шейки колесной оси 130 мм) от мощности индукционного нагрева для разных величин натяга: кривые 1,2,3 соответствуют натягам d =30;40;50 мкм, ω=5 кГц. Характерной чертой всех кривых является наличие области, где температура разъединения кольца с осью слабо зависит от мощности нагрева и области, где температура разъединения пропорциональна мощности нагрева. Очевидно, что температура разъединения носит пороговый характер, т. е. сколько зажженной спичкой не грей кольцо не снимешь. Другими словами, при значениях мощности меньше пороговой разъединение деталей не происходит. Отмечаем, что область независимости (или слабой зависимости) температуры разъединения деталей от мощности индукционного нагрева с ростом величины натяга уменьшается, а для натяга 50 мкм, скорее всего, этой области не существует.

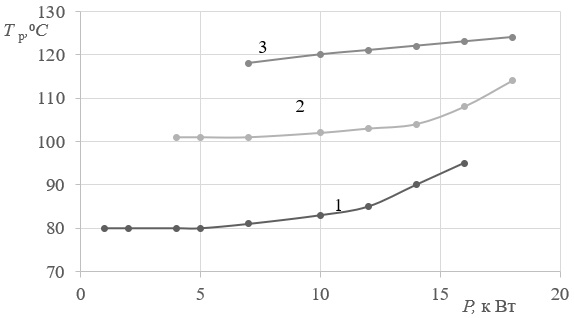
Рис. 2. Зависимость температуры разъединения кольца №42726 от мощности индукционного нагрева.
Натяги: 30 мкм для №1, 40 мкм для № 2, 50 мкм для №3.
Частота электромагнитного поля составляла 5 кГц.

На рис. 3 представлен график зависимости мощности, при которой происходит разъединение деталей, от величины натяга. Этот график построен по данным, представленным на рис. 2: данные по координате мощности являются пороговыми величинами, при которых происходит разъединение деталей. Расчетные точки графика (кривая «1») зависимости мощности нагрева от величины натяга описывается параболической кривой. Для втулки уплотнения двигателя 1ДТ.003.3 мы получили из расчетов зависимость, отображенной кривой «2». Как видно из графика для величины натяга 50 мкм квадратичная зависимость не выполняется. Можно констатировать, что для относительно малых мощностей индукционного нагрева, что соотносится с малыми величинам натяга, имеет место параболическая зависимость температуры разъединения от мощности индукционного нагрева.  Для высоких значений мощности и значений натяга указанная зависимость не выполняется.

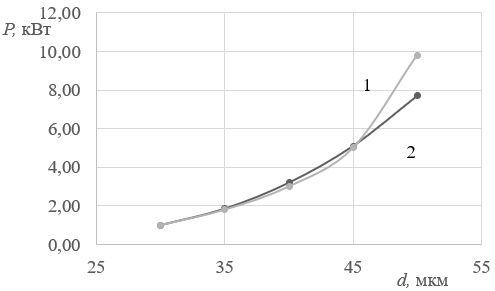
Рис. 3. Зависимость температуры разъединения кольца и оси от величины натяга: по данным рисунка №2 (кривая «2,»).
Кривая «1» — расчет по квадратичной зависимости, ω=5 кГц

В расчетах графиков рис. 2 мощность изменяли с помощью изменения тока индуктора. Но мощность, выделяемая в кольце, при индукционном нагреве зависит также от частоты этого тока [8], как P≈√ ω, где ω ̶ частота переменного тока индуктора. Мы рассчитали зависимость температуры разъединения кольца и оси для кольца подшипника № 42736 (подшипник локомотивной ступицы) при d=30 мкм, ω=10 кГц. Видно, что температура разъединения пропорциональна мощности индукционного нагрева, а области независимости температуры разъединения от мощности не существует.

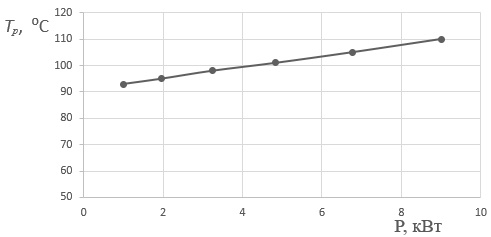
Рис. 4. Зависимость T_р(P) для кольца № 42736, натяг 30мкм, ω=10кГц

Чтобы объяснить указанные закономерности рассчитали зависимости распределения температуры по сечению кольца для двух вышеозначенных областей — слабая и относительно высокая мощность индукционного нагрева: первая область соответствует слабой зависимости температуры разъединения от мощности нагрева и вторая область, где температура разъединения пропорциональна мощности нагрева.

На рис. 5 представлен график распределения температуры по сечению кольца № 42726 в момент его разъединения с осью: линия Т1 соответствует области слабой зависимости температуры разъединения от мощности, а линия Т2 относится к области, в которой температура разъединения растет с ростом мощности. В данном случае речь идет о кольце с натягом 40 мкм, ω=5 кГц.

Видно отличие распределения температурных зависимостей по сечению кольца. Можно предположить, что для T1 кольцо расширяется постепенно, как целое, и такой съем можно определить как термомеханический. Мы неоднократно наблюдали, как в некоторых случаях, когда кольцо не снималось, то вызывали газосварщика, тот делал мощную длинную струю и плавными движениями грел по кругу кольцо, и оно снималось. В области, где температура Tр зависит от мощности, кольцо снимается быстро, а ось при этом нагревается слабо: в момент разъединения ось имеет температуру 27⁰C, а начальная температура оси равна 20⁰С.

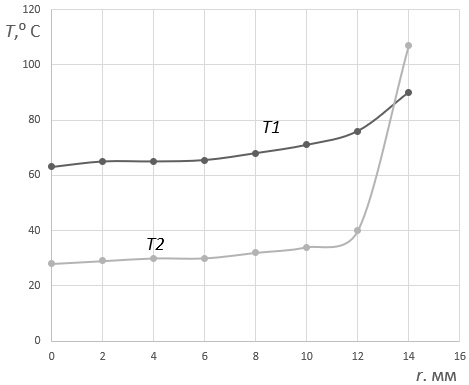
Рис. 5. Распределение температуры по сечению кольца №42726.
График T(r) рассчитан для натяга d=40 мкм рисунка №2

Мы связываем такое поведение T(r) с зависимостью параметра температуропроводности a=λ/(cγ) от температуры. Параметр, который определен уравнением (1). Также следует иметь в виду зависимость от температуры модуля Юнга E. В наших расчетах принципиально учитывались температурные зависимости указанных выше параметров.

Известно [9,10], что оба параметра уменьшаются с ростом температуры, для сталей эта зависимость начинает проявляться при температуре 80⁰C и выше. При более низких температурах указанные параметры практически не зависят от температуры, что ведет к независимости температуры съема от мощности. Когда температура приближается к 100 ⁰C, то уменьшение параметра a приводит к затруднению изменения температуры по сечению кольца, в то же время температура на поверхности растет. Сравнение положения профилей в области от 0 до 12 мм: для Т1 профиль сосредоточен в области 64 ⁰С, профиль Т2 в этой области сосредоточен при 27 ⁰С, а начальная температура в при расчетах равна 20 ⁰С. Можно сказать, что для кольца с состоянием T2 температура во внутренней части кольца как бы «замораживается». В области T2 скорость роста температуры на внешней поверхности кольца более чем в 4 раза превышает скорость изменения температуры во внутреннем объеме кольца. Рост температуры в приповерхностном слое, способствует быстрому «растягиванию» приповерхностного слоя кольца, что приводит к снятию натяга (d=0).

Заключительная часть. Для объяснения параболической зависимости мощности, при которой натяг зануляется (d=0) от величины натяга, используем закон Гука [11] для оценочных вычислений. Для этой области, где термофизические характеристики почти не меняются с температурой, указанный закон можно применить. При относительно медленном нагревании кольцо нагревается и расширяется, происходит работа против упругой силы F=kr, где k – коэффициент упругости, r — координата по радиусу кольца. Работа A по снятию натяга определится интегралом

 A=∫krdr                                       (4).

Интеграл определяем в пределах от 0 до d, т.е. до состояния, когда натяг «снимается». После интегрирования получим

A=kd²/2                                       (5).

Теперь из (3) и (5) вытекает P̶ ~d², что подтверждают данные рис. 3. Исключение относится к относительно большим значениям натяга, где «работает» другой механизм разъединения кольца с осью. Это требует дополнительных исследований.

Данные рис. 2 позволяют сделать вывод, который имеет значение для технических приложений индукционного нагрева, применяемого в разных отраслях машиностроения. Дело в том, что в значительной области мощностей можно выбрать такую, при которой разъединяются кольца с разным натягом. Поскольку для внутренних колец подшипников, используемых в ОАО РЖД, существует подчас значительный разброс в величинах натягов [12,13], то возможность снятия колец с разбросом величин натягов при одном и том же значении мощности представляет значительный производственный интерес. При этом надо отметить, что наши вычисления для внутренних колец подшипников показывают, что это возможно: предел температуры разъединения кольца с осью, установленный нормативами ОАО РЖД (120 ͦС), не превышен в значительном диапазоне мощности (рис. 2). Для таких температурных профилей вполне можно ввести понятие средней температуры [14], которое используют при выборе нагрева для получения определенной величины натяга. Указанное обстоятельство позволяет говорить о необходимости создания такого типа индукционных нагревателей, в которых необходимо учитывать зависимость мощности съема кольца (и ему подобных деталей) от величины натяга. Возможность работы с одним значением мощности нагрева, изменяя только время нагрева, позволяет ввести в память устройства предельный режим нагрева для данной детали. Выход за рамки этого режима, т.е. нарушение регламента операции, может быть занесено в память нагревателя, как «ЧП».

Выводы. Таким образом результаты нашего предыдущего исследования и представленной здесь работы описывают физические процессы, происходящие в цилиндрической детали, сопряженной натягом с осью, при индукционном нагреве. Показано, что в зависимости температуры внешней поверхности кольца, при которой кольцо снимается без натяга, от мощности индукционного нагрева существуют две области.  Для относительно малых мощностей температура разъединения практически не зависит от мощности, в этом диапазоне мощность пропорциональна квадрату величины натяга. При высоких значениях мощности температура разъединения пропорциональна мощности.

При увеличении частоты электромагнитного поля температура разъединения деталей начинает зависеть от мощности и пропорциональна мощности, а области независимости температуры разъединения деталей от мощности, по-видимому, не существует.

Хотя расчетно-теоретическая часть проведена на простой модели кольца, сопряженного натягом с осью, выводы будут полезны для широкого круга сопряженных с осью деталей, например, для бандажей станов холодного волочения труб, бандажей центров колесных пар локомотивов, ходовых колец транспортных средств, в т. ч. эскалаторов метрополитенов. По всем указанным деталям у нас есть опыт внедрения индукционных нагревателей.

Важным для технологического аспекта машиностроительного производства является вывод о необходимости при проектировании и производстве высокочастотных индукционных нагревателей учитывать сильную зависимость температуры съема от величины натяга сопряженных деталей. Необходимо иметь возможность плавно менять и регистрировать мощность и время нагрева.

СПИСОК ИСТОЧНИКОВ

1. Дудин В. И., Лелехов С.А., Сушко А. В., Фещуков А.Н. Деформация цилиндрических деталей, сопряженных с осью, при индукционном нагреве. Вестник машиностроения, 2021, №12, с. 33.
2. Владимиров В.С. Уравнения математической физики. изд. 5, М., Наука, 1988
3. Князева. А.Г. Учебное пособие по курсу «Теплофизические основы современных методов термообработки», Изд. Томского политехнического университета. 2012.
4. Лозинский М. Г. Промышленное применение индукционного нагрева. Изд. Академии Наук СССР, Москва, 1958
5. Справочник «Физические величины». М.: Энергоатомиздат, 1991
6. Steinmetz K. Theory and calculation of transient electric phenomena and oscillaition. N.Y., Mc Crow Hill Book Co. 1920.
7. Ермоленко Д. В., Юферов Л. Ю., Рощин О. А. Результаты испытаний резонансной системы передачи электроэнергии для индукционного нагрева рельсов стрелочного перевода. Вестник ВНИИЖТ, т. 78, №1, с. 48–53.
8. Котельников И.А., Черкасский В.С. // Электронный учебник. Скин-эффект в задачах. 2014. С. 34
9. Справочник «Марочник сталей и сплавов» под ред. Зубенко А. С. М.: Машиностроение, 2003, с. 784.
10. Агажанов А.Ш., Савченко И.В., Самошников Д.А., Ставкус С.В. Дутова О.С. Коэффициент температуропроводности стали 16Х12 в широком интервале температур. Вестник НГУ, серия: Физика. 2013, том 8, выпуск 3, с. 163.
11. Феодосьев В.И. Сопротивление материалов. М.: Наука, 1986, с. 34
12. Электрические машины электропоездов. Общее руководство по ремонту. 104.03.00672-2009 КО. ТД «УралЮрИздат», Екатеринбург, 2019.
13. ЦТ-330. Инструкция ТО и ТР узлов с подшипниками качения локомотивов. МПС РФ от 11.07.1995г.
14. Дунаев.П.Ф., Леанков О.П., Варламова Л.П. «Допуски и посадки», М.: «Высшая школа», 1984, 51.